백준 2957번 C++

2957 번

문제에서 설명한 대로 이진트리를 구성해서 풀게되면 평균 O(nlogn)으로 풀 수 있다고 예상한다.

하지만 다음처럼 트리가 한쪽으로만 발달하는 최악의 경우 O(n^2)의 복잡도를 갖게된다.

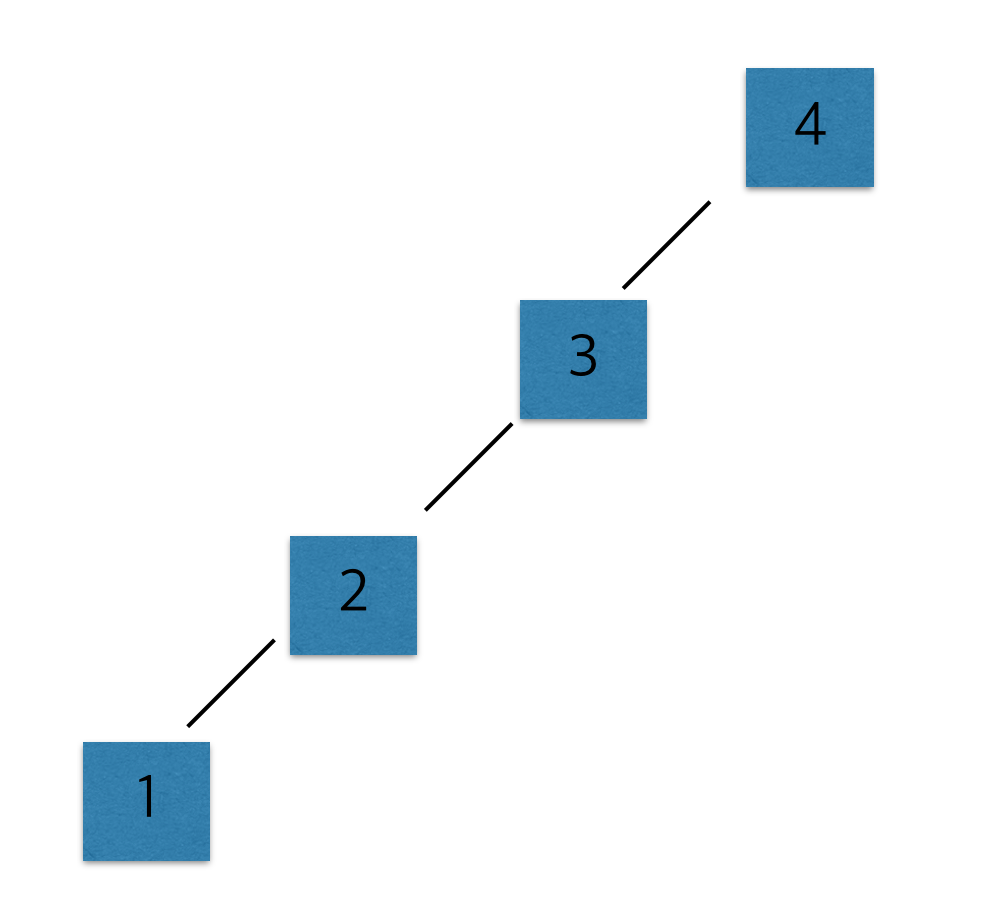
입력 개수가 30만개이기 때문에 제곱 시간복잡도로는 1초안에 문제를 풀 수 없다.

이진트리의 성질

4가 들어갈 자리를 찾아보자.

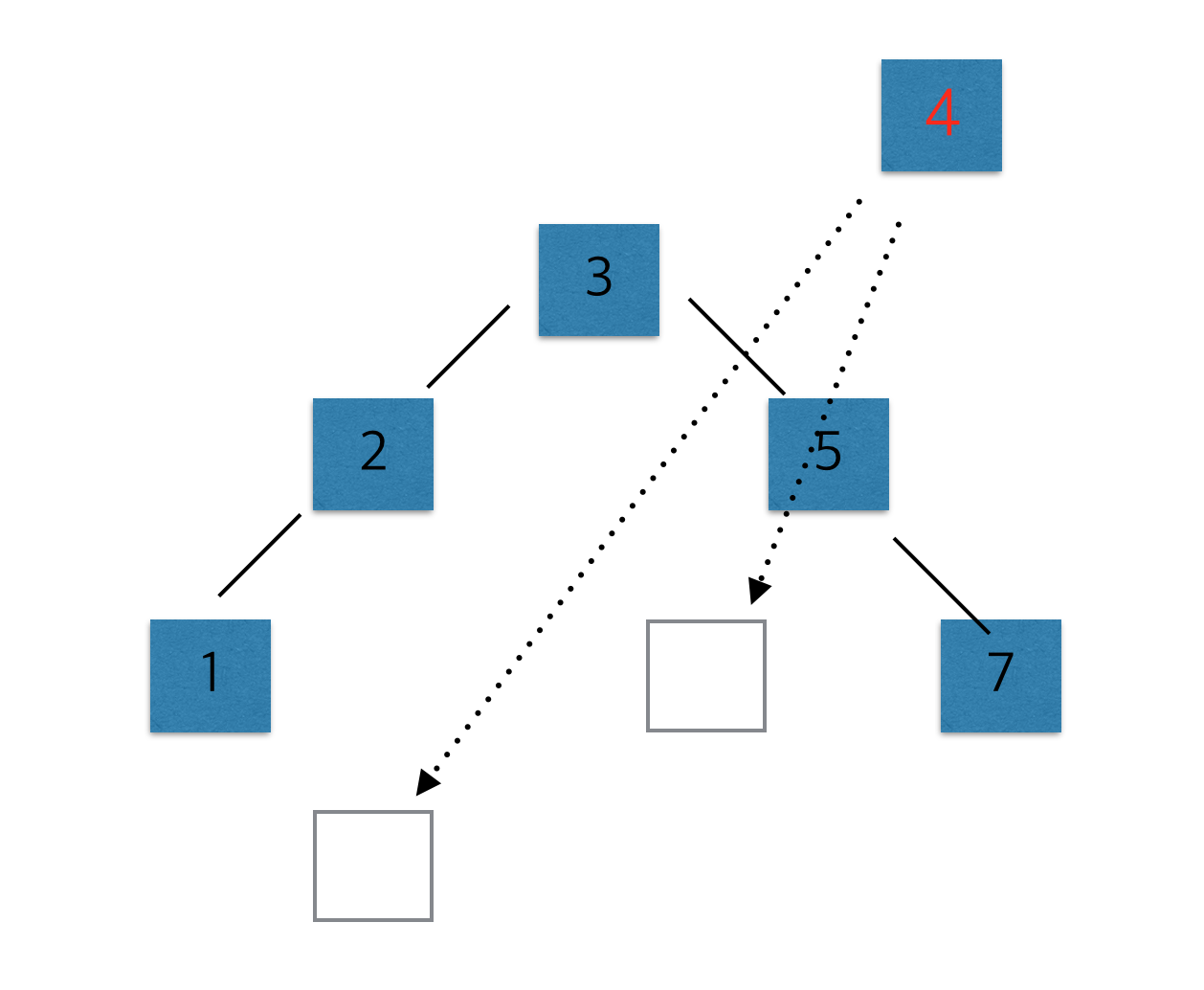
이진트리는 삽입 순서대로 트리가 구성되기 때문에 정렬된 배열처럼 완벽한 순서는 없어보인다.
[명제 1]이진트리는 새로운 값을 입력할 때 분명 보다 {작은 값보다는} 오른쪽에 위치한다.
[명제 2]이진트리는 새로운 값을 입력할 때 분명 보다 {큰 값보다는} 왼쪽에 위치한다.
그럼 임의의 트리에 4라는 값을 입력한다고 할 때 4의 위치를 추정해보자.
만약 3이 존재한고, 3의 오른쪽이 비어있다면 반드시 3의 바로 오른쪽에 올 것이다.

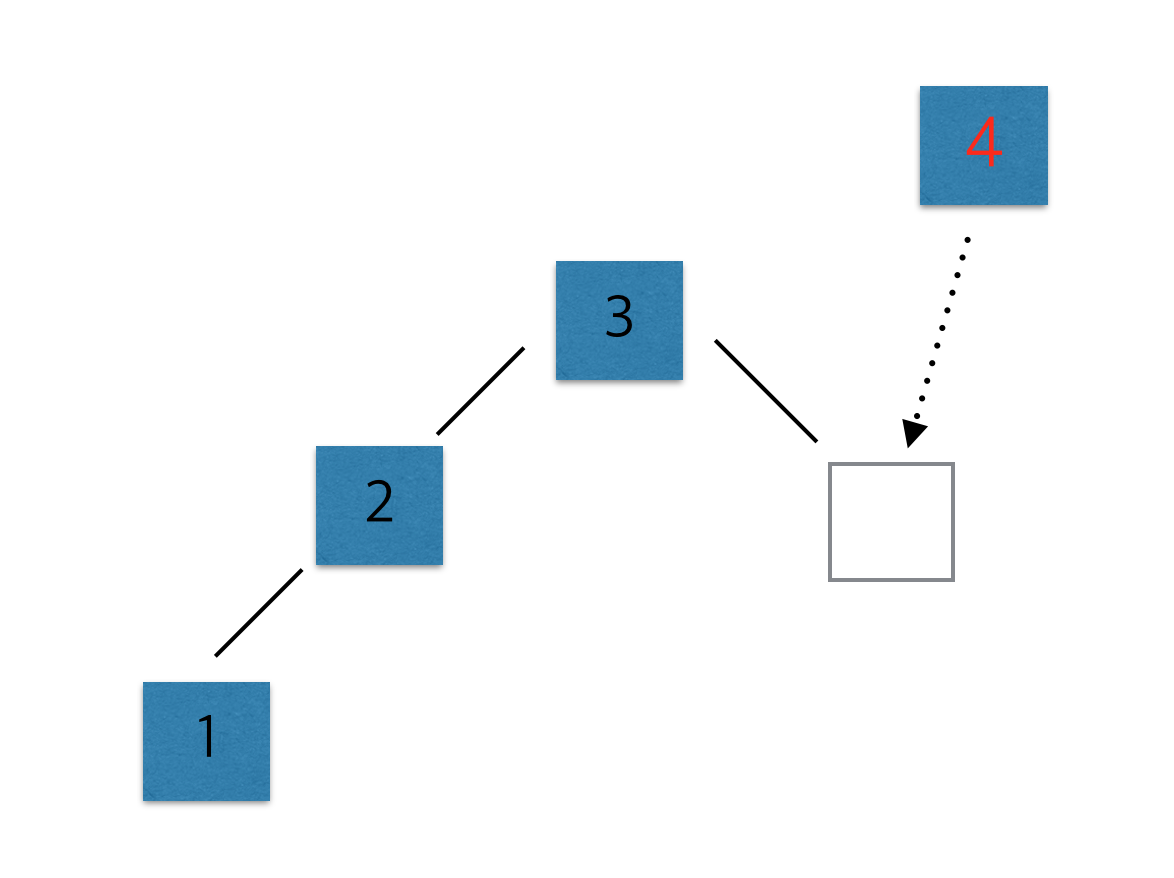
만약 3이 존재하지 않고 2 혹은 1이 있다면 그리고 오른쪽 값이 비어있다면 반드시 그 자리에 올 것이다.
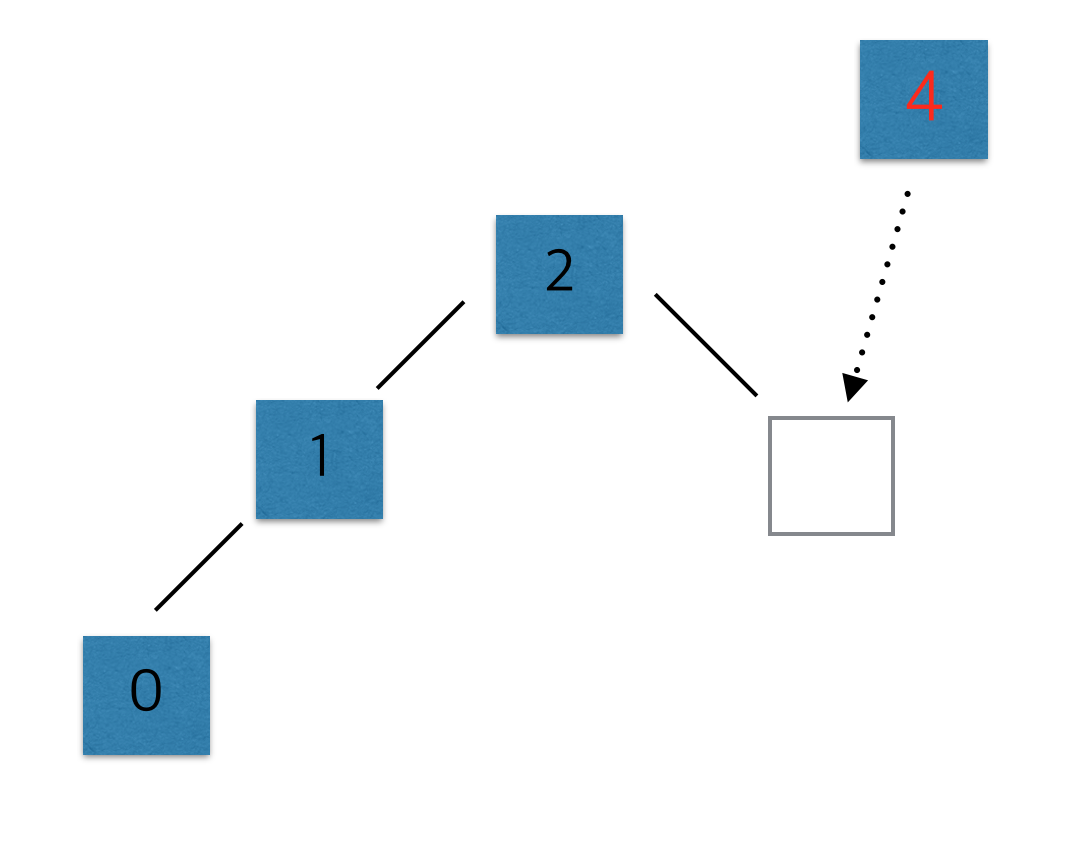
더 정확하게 말해서 4보다 작은 값이 존재하고 그 중에서 가장 큰 값의 오른쪽에 올 것이다. 단 비어있기만 하다면.
동일한 원리로 만약 5가 존재하고, 5의 왼쪽이 비어있다면 반드시 5의 바로 왼쪽에 올 것이다.
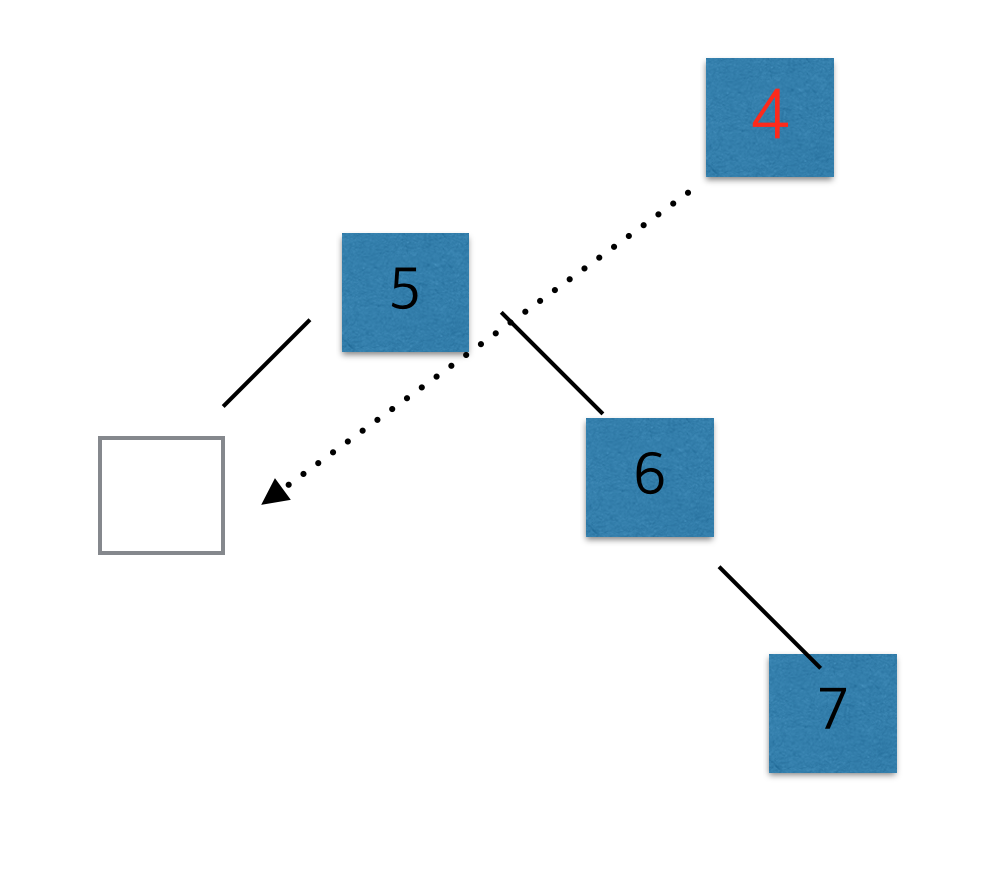
마찬가지로 5가 존재하지 않고 6, 또는 7이 있다면 그리고 온쪽이 비어있다면 반드시 그 자리에 올 것이다.
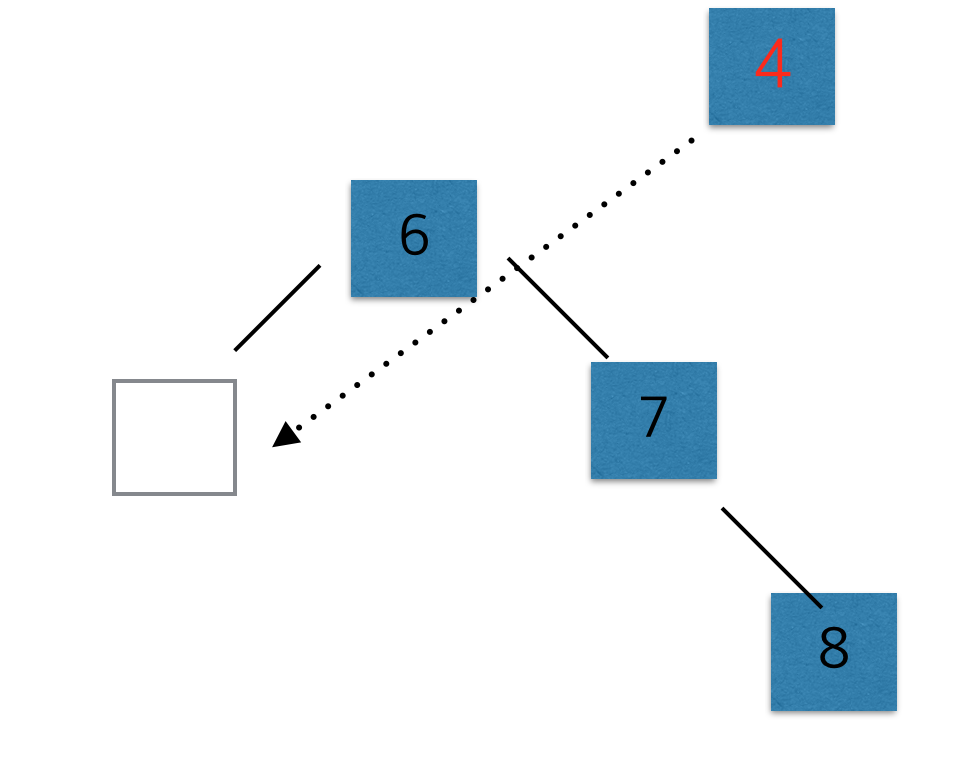
더 정확하게 말해서 4보다 큰 값이 존재하고 그 중에서 가장 작은 값의 왼쪽에 올 것이다. 단 비어있기만 하다면.
마지막으로 큰 값과 작은값이 모두 존재한다면 비어있는 값에 들어가게 될 것이다.
마지막 조건을 다시 한번 생각해볼 필요가 있는데, 이 문제의 핵심이다. {비어있는 값}을 다른 말로 바꾸어 보자 {루트로 부터 멀리 떨어져있는 값}

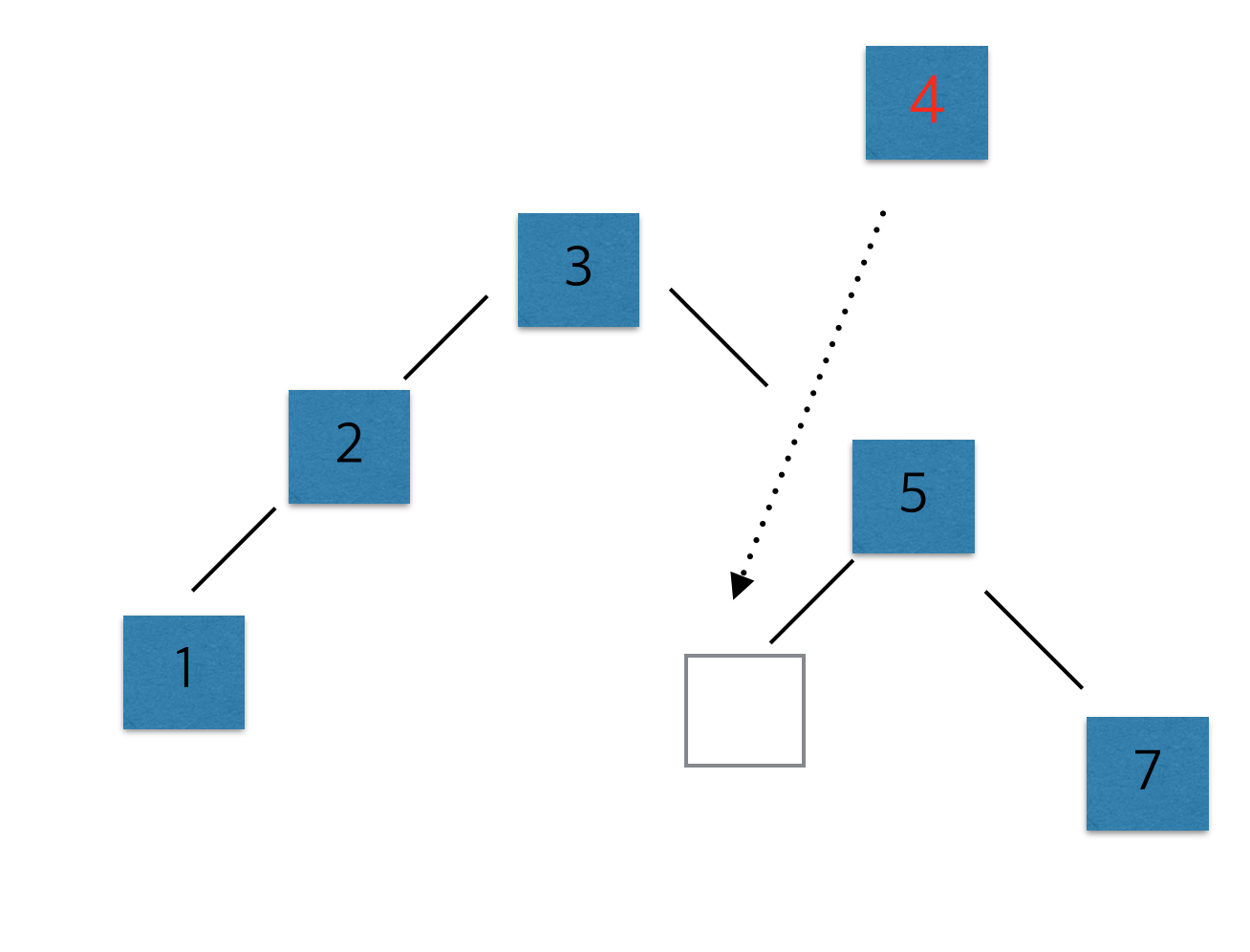
위의 그림 처럼 4보다 작은값이 존재하고(여기에서는 3) 4보다 큰 값이 존재하면서 3의 오른쪽이 비어있을 수는 없다. 4보다 큰 값(여기서는 5)이 3의 오른쪽에 위치하게 된다. 즉 여기에서는 5의 왼쪽에 오게 된다. {루트로부터 멀리 떨어져있는 값}이란 말을 기억해보자.

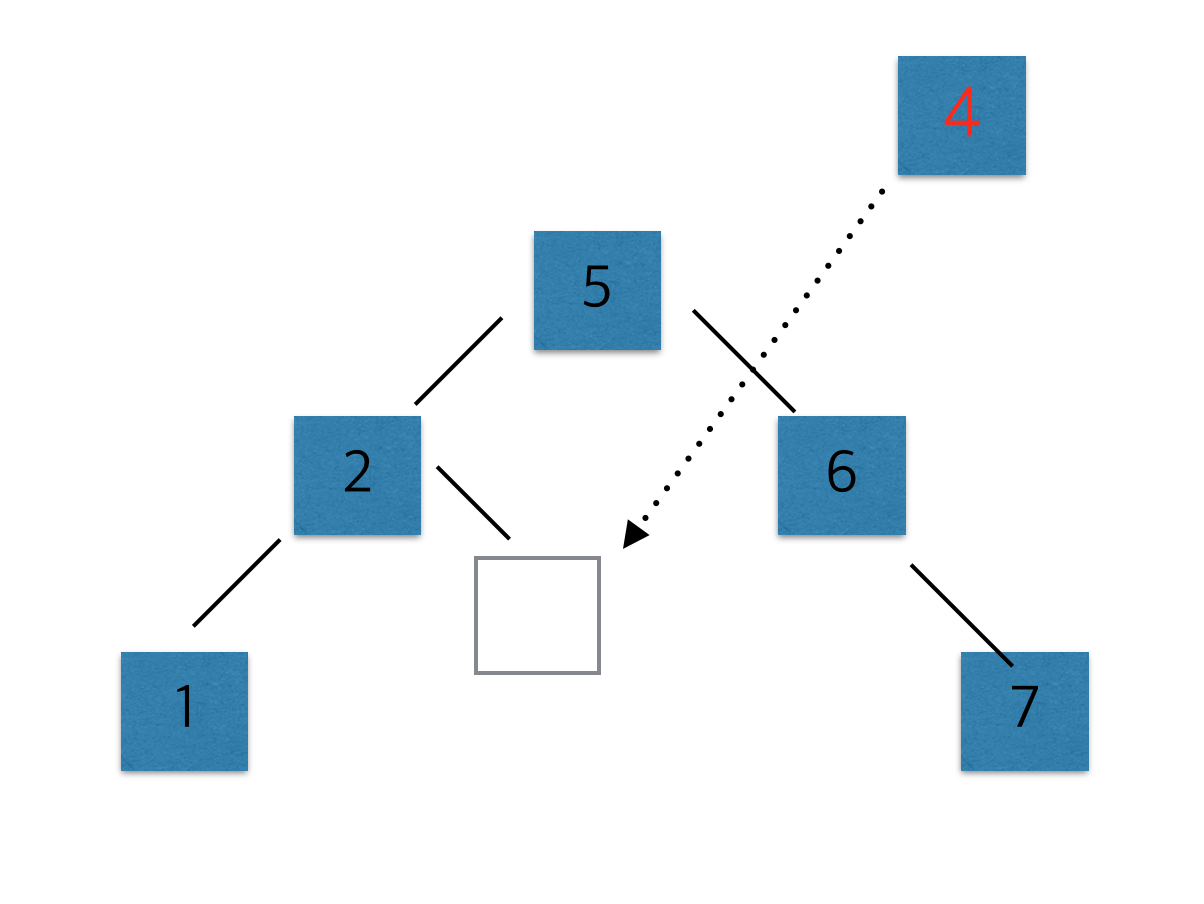
이번에는 그림이 좀 달라졌다. 5도 존재하고 2도 존재한다. 이 때 5의 왼쪽은 채워져있으며 2의 오른쪽은 비워져있다. 5보다 작은 2가 있으므로 당연히 채워질 수 밖에 없다. 이때에도 당연히 입력값 4는 2의 오른쪽에 오게되고 이는 {루트로부터 멀리 떨어져있는 값}에 해당한다.

빠른 이진 트리

자 이제 위에서 공부한 내용으로 빠른 이진 트리를 구성하려고 한다.

삽입 값 보다 큰 값중에 루트까지 거리가 가까운 값 == 입력값보다 큰 값중에서 가장 작은 값
삽입 값 보다 작은 값중에 루트까지 거리가 가까운 값 == 입력값보다 작은 값 중에서 가장 큰 값.
두가지 테크닉이 가능한데 둘 중 아무거나 사용해서 풀어보겠다.
여기서 입력값보다 작은 값 중에서 가장 큰 값.
입력값보다 큰 값 중에서 가장 작은 값이라는 용어를 기억하자
아래에서 방금 설명한 내용을 lower_bound와 upper_bound란 용어를 사용해서 풀 것이다.

STL Map

C++의 STL중 Map이라는 컨테이너를 사용해서 문제를 풀 것이다. Map은 이진 트리를 사용해서 검색을 배열이나 링크드 리스트에 비해서 훨씬(logn)빠르게 수행한다.
Map에 대해 더 궁금한 게 있다면 이전 포스팅을 참고하자

맵은 레드블랙트리로 구성되어 있다.

레드 블랙트리는 균형잡힌 이진 트리로서 불균형한 이진 트리를 보완하기 위해서 새롭게 만든 트리이다. 이 부분은 잘 몰라도 문제를 풀 수 있다.

lower_bound(int x) : x가 있다면 x를 반환하고, x가 없다면 x보다 큰 값중 가장 작은 값을 반환한다.
upper_bound: x보다 큰 값중 가장 작은 값을 반환한다.
iterator : 사실 위에서서 값이라고 했지만 정확히는 포인터를 반환한다고 알면 된다.
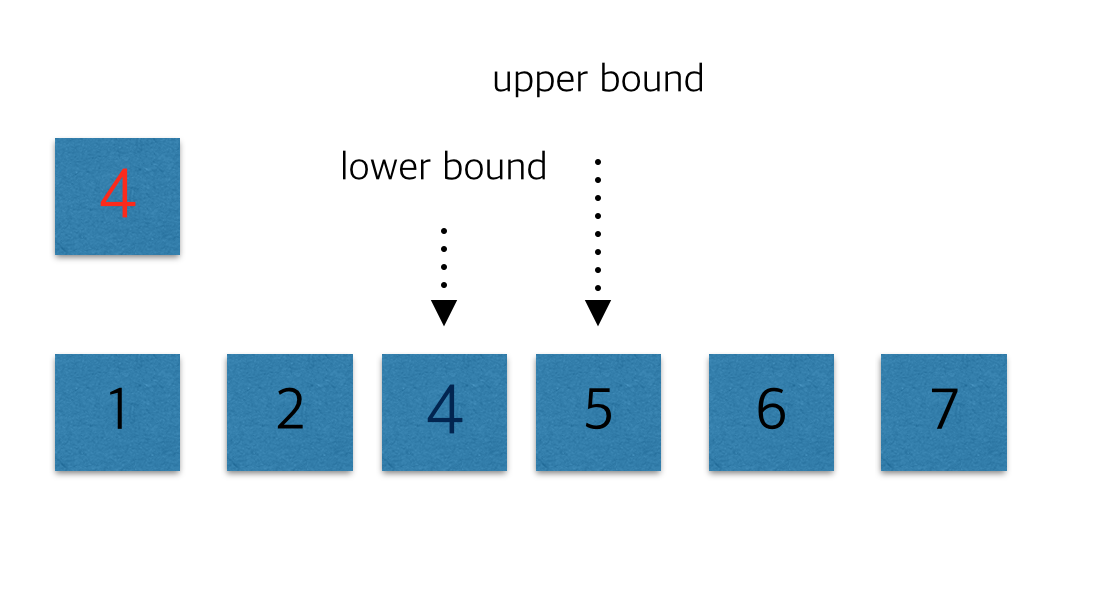
만약 4가 없을 경우에는 lower_bound는 5를 반환할 것이다. 이때 lower_bound는 포인터라고 했으므로 lower_bound에서 1만큼 빼주게 되면 2라는 값을 찾을 수 있다. (lower_bound -> second)로 접근

유의할 점

int와 long long int를 구별해서 써야할 시기가 왔다. 알고리즘 문제를 풀 때 정답을 맞추지 못한다면 int 값을 넘어가는 범위인지 잘 생각해야한다. 또 printf()에서도 long long int를 사용했다면 형식을 “%d”가 아닌 “%lld”로 접근해야 한다.
cin, cout은 속도가 많이 느린 편이다. printf, scanf를 대신 사용하자.
소스코드는 다음과 같다.

#include <stdio.h>
#include <map>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;


void insert(map<int, long long int>& v, vector<long long int>& sum, int x)
{
    map<int, long long int>:: iterator lower_bound;
    map<int, long long int>:: iterator upper_bound;



    lower_bound = --v.lower_bound(x);
    upper_bound = v.upper_bound(x);
    long long int count = 0;
    count = max(lower_bound -> second, upper_bound -> second) + 1;
    v.insert(pair<int, long long int>{x, count});
    if(sum.size() > 1)
    {
        sum.push_back(sum[sum.size() - 1] + count);
    }
    else
    {
        sum.push_back(count);
    }
    return ;
}


int main()
{
    map<int, long long int> tree;
    tree.insert(pair<int, long long int>{0, -1});
    tree.insert(pair<int, long long int>{300001, -1});
    int n;
    int m;
    vector<long long int>sum;
    scanf("%d", &n);
    while(n--)
    {
        scanf("%d", &m);
        insert(tree, sum, m);
    }

    for(long long int x: sum)
    {
        printf("%lld\n", x);
    }
    
    
}