이진트리 탐색

이진트리는 탐색에 최적화되어있다. 링크드 리스트가 평균 탐색 비용이 N/2이라면 이진트리는 균형 잡힌 N개의 노드에 대해서 최대 탐색 비용이 log(N). 이때 균형 잡혔다는 조건이 중요한데 트리가 한쪽에 편향되어 있지 않고 양쪽으로 균형잡히게 발달한 경우를 얘기한다. 만약 한쪽으로만 편향되어 있는 경우에는 최악으로 평균 N/2 즉 O(N)으로 링크드 리스트와 같다.

Map

Map은 보통 문자열과 숫자를 저장하는 노드(C++에서는 구조체 혹은 클래스)를 만들어서 같이 관리하는 방식입니다. Vector를 사용해서 저장하는 것보다 서로 다른 값들 사이에 연관성을 명확해진다는 장점이 있습니다.
Map은 보통 위에서 말한 것처럼 이진트리를 사용해서 연결관계를 유지합니다. 물론 문자열과 숫자가 아니라 문자열과 문자열, 숫자와 숫자, 어떤 조합이든 상관 없습니다.

Map 방식으로 저장한 10만개의 문자열과 해당하는 숫자로 이루어진 이진트리가 있다고 해봅시다. 이때 문자열을 주어지고 해당하는 숫자를 찾으라고 했을 때 벡터로 구현했다면 평균 5(10/2)만번의 탐색비용이 발생할 것입니다. 그렇지만 이진트리를 사용했을 경우 약 17번의 탐색으로 찾을 수 있으니 엄청난 성능입니다.

• 벡터 탐색
  

• 이진트리 탐색
  

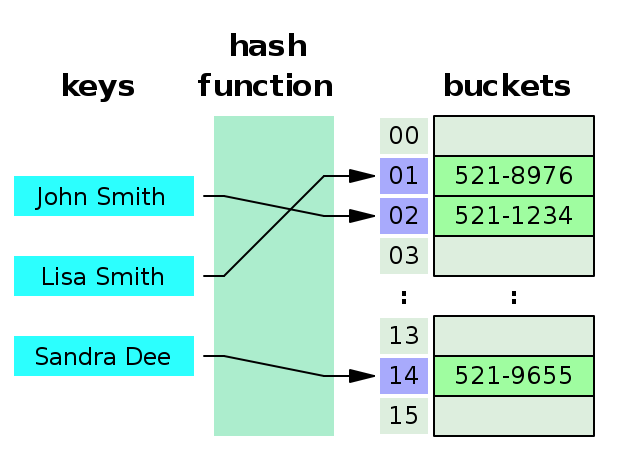
해쉬 테이블

해쉬 테이블은 위에서 말한 조합중 문자열과 숫자를 묶어줄 수 있는 자료구조 입니다. 당연히 Map + 이진트리보다 더 뛰어난 성능을 가지고 있습니다. 해쉬 함수를 통해서 문자열을 숫자로 바꿔줍니다. 그리고 이 숫자를 가지고 배열의 인덱스로 삼아 원하는 숫자값을 저장할 수있습니다.
해쉬테이블의 경우 조회 연산의 비용이 O(1)로 0에 가깝습니다.

• 해쉬 테이블
  

Using 선언과 지시자

선언과 지시자라는 이름이 좀 낯섭니다.

선언

using 선언은 다른 네임스페이스에서 선언된 이름에 대한 지역 동의어를 만들어 주는 것입니다.

지시어

using 지시자는 다른 네임스페이스에 있는 모든 이름을 using 지시자의 영역에서 사용할 수 있게 해줍니다 using 선언과 달리 using지시자는 자신의 앞과 뒤에 선언된 모든 이름을 가져옵니다.